本文對曲線頂管的最重要參數——最小曲線半徑進行了探討,得出最小曲線半徑與管段長度、管徑成正比,與木墊片厚度成反比的關系。另外還指出曲線半徑還受土體承載力的制約,要防止管道在施工中發生縱向失穩。
曲線頂管是頂管的前沿技術,只有當頂管被工程界廣泛采納后才會提出曲線頂管問題。目前曲線頂管各國尚處于研究發展階段,有些曲線目前已能施工,有些曲線還不能。例如彎曲半徑太小,有可能造成管道失穩,管道裂縫等嚴重后果。曲線頂管多用于舊城區的改造,舊城區馬路彎曲,管道一般沿馬路敷設,這就需要采用曲線頂管。另一種情況是過江過河的混凝土頂管,有時為了減少投資,把管軸線設計成倒虹管或者拋物線形狀,這也需要采用曲線頂管。曲線頂管比較適合于混凝土管。曲線頂管用于鋼管,則需要很大的彎曲半徑,而且必須有中繼環。
管道的彎曲半徑的大小與土質、管徑、頂力有關。土體承載力高,彎曲半徑可以小一點;反之,承載力低,彎曲半徑要大一點。管道口徑大,彎曲半徑要大一點;反之,管道口徑小,彎曲半徑可以小一點。管段較長,彎曲半徑要大一點;反之,管段較短,彎曲半徑可以小一點。施工頂力較大,彎曲半徑要大一點;反之,頂力較小,彎曲半徑可以小一點。
一、 混凝土管最小彎曲半徑分析
最小彎曲半徑時忽略土體承載力和施工頂力影響,僅就管道口徑大小、管段長度、木墊片的厚度三者與最小彎曲半徑的關系進行分析。曲線頂管的軸線,從宏觀上看是曲線,實際上是折線,是多邊形的一部份,多邊形的邊就是管段長度。從圖1可知多邊形的邊、角、半徑有如下關系:
α=l/R
式中 α—中心角(弧度);
l—邊長;
R—多邊形外切圓半徑。
曲線頂管中把管段的長度看成是多邊形的邊,管段對應的中心角就是多邊形的中心角,管軸線就是多邊形的外切圓。
假設管道內徑為d,壁厚為t,管段長度為l,木墊片厚度為b,并假設管道壁厚是內徑的1/10,木墊片允許最大壓縮率是50%。
即 t=d/10
S=b?50%
從圖1可知,管段間的轉角與管段對應的中心角相等。則曲線的最小彎曲半徑可按下式計算:
Rmin=l(d+2t)/(b-s)或Rmin=12ld/5b
式中 Rmin—最小彎曲半徑(m);
l—管段的長度(m);
d—管道內徑(m);
t—管道壁厚(m);
b—木墊片厚度(m);
s—木墊片最小壓縮高度(m)。 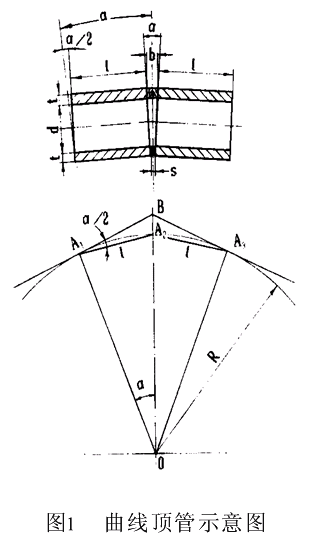 由上式確定的不同管徑混凝土管的最小彎曲半徑見表1。彎曲半徑太小,會使管段上應力過于集中,使管道混凝土裂縫。這是要力求避免的。
由上式確定的不同管徑混凝土管的最小彎曲半徑見表1。彎曲半徑太小,會使管段上應力過于集中,使管道混凝土裂縫。這是要力求避免的。
二、鋼管頂管的最小彎曲半徑
無中繼環的鋼管不能用于曲線頂管。鋼管曲線頂管的最小彎曲半徑的大小主要取決于中繼環布置的間距和中繼環的允許轉角。目前鋼管頂管沿用的老式中繼環允許轉角很小,因此不宜用于曲線頂管。組合密封中繼環研究成功后,允許中繼環有較大的轉角,因此可用于曲線頂管。已知中繼環的允許轉角和間距,鋼管管道的最小彎曲半徑可按下式計算:
Rmin≥L/2sin(kα/2)
最小彎曲半徑參考值 單位:m 表1
| 公稱管徑(mm) | 木墊片厚0.03 | 木墊片厚0.02 | ||
管段長2.0 | 管段長2.5 | 管段長2.0 | 管段長2.5 | |
| 800 | 128 | 160 | 192 | 240 |
| 1000 | 160 | 200 | 240 | 300 |
| 1200 | 190 | 260 | 288 | 360 |
| 1400 | 224 | 280 | 336 | 420 |
| 1600 | 256 | 320 | 384 | 480 |
| 1800 | 288 | 360 | 432 | 540 |
| 2000 | 320 | 400 | 480 | 600 |
| 2200 | 352 | 440 | 528 | 660 |
| 2400 | 384 | 480 | 576 | 720 |
| 2600 | 416 | 520 | 624 | 780 |
| 2800 | 448 | 560 | 672 | 840 |
| 3000 | 480 | 600 | 720 | 900 |
| 3200 | 512 | 640 | 760 | 960 |
| 3400 | 544 | 680 | 816 | 1020 |
| 3600 | 576 | 720 | 804 | 1080 |
| 3800 | 608 | 760 | 912 | 1140 |
| 4000 | 640 | 800 | 960 | 1200 |
說明:
1.假定土體有足夠的承載力。
2.假定頂力在允許范圍內。
3.表中未考慮施工偏差對彎曲半徑的影響。
式中
Rmin—最小彎曲半徑(m);
α—中繼環的允許轉角,取α=1°;
k—系數,k=0.5;
L—中繼環間距(m)。
如果中繼環間距L=60m,則彎曲半徑Rmin≥6875m。
三、管道的側向力
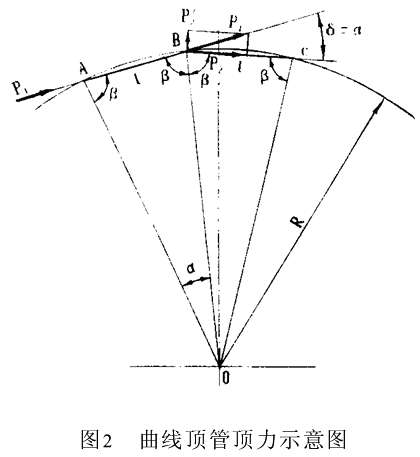
曲線頂管的頂力可分成軸向力和側向力兩部分,下面分析作用在管段上的側向力的大小。由圖2可知,折線轉向角δ是∠ABC的補角。
因為 ∠ABC=2β所示
δ=180-2β
α=180-2β
δ=α
假設忽略管壁摩阻力,并假設AB管段的軸向頂力是P1,則BC管段的軸向頂力和側向分力是
p2=p1ctgα
p′2=p1tgα
式中 p2—下一管段的軸向頂力;
p′2—下一管段的側向分力。
由此可見,曲線頂管存在側向分力,因此要驗算土體的承載力。如果承載力不夠,管軸線會因此失穩,側向分力使管道靠向曲線外側,并作用在土體上,還會使管道的頂進阻力增加。因此曲線頂管在頂力配置時要考慮管道摩阻力增加的因素。
已知彎曲半徑R和管段長度l,就可以求得α。根據軸向頂力的大小,就可求得側向分力。再根據μ值,即可求得管段的附加摩阻力。
四、頂力的調正
曲線頂進時,管段的允許頂力要折減。折減系數與管段轉角有關,混凝土管還與木墊片的彈性模量、木墊片的厚薄有關。曲線頂管不但會使混凝土管的允許頂力下降,而且還會使管道總頂力增加。如果中繼環設計頂力不變,則曲線頂管中繼環的數量要比直線頂管多。
管道進入曲線段,管段間的頂力傳遞面靠向曲線內側(見圖2),因此中繼環進入曲線段后頂力要調正,使中繼環的頂力合力中心與其他管段傳力一致。調正的辦法是曲線外側的中繼油缸要封住,即部份油缸不使用。停用油缸數量可通過計算。最簡單的辦法是,觀測中繼環轉角有無變化。轉角增加,表示要增加停用的油缸,合力中心還要靠向曲線內側;轉角減小,表示停用的油缸太多了,需要減少;只有當轉角不增不減,或者變化不大時,認為調正是正確的。
中繼環的頂力調整降低了中繼環的實際使用頂力,因此中繼環的允許使用頂力還要比設計頂力低,頂力配置時要考慮這一因素。
 五、曲線頂管的超挖
五、曲線頂管的超挖
曲線頂管,要求直線形的管段沿圓弧移動(見圖4),因此必然要超挖。超量大小與彎曲半徑、管道直徑、管段長度有關。超挖量可按下式計算:
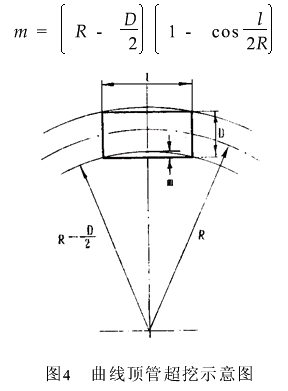
式中 m—半徑方向超挖量(m);
R—彎曲半徑(m);
D—管道外徑(m);
l—管段長度(m)。
例如管道外徑2.4m,管段長2.5m,彎曲半徑400m,則:
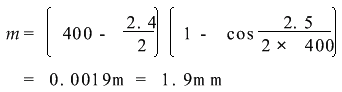
可見混凝土曲線頂管中存在超挖的問題。對硬土來說這是曲線頂進的需要,否則管段很難轉向,摩阻力也會因此而增加。對于軟土情況就會好一些。所以在硬土中頂管,要考慮超挖的方法。但鋼管頂管因為設計的彎曲半徑很大,超挖量就很小,可以忽略不計。
六、曲線頂管測量
曲線頂管的測量是曲線頂管的關鍵技術問題。曲線頂進時因管內外無法通視,因此必須改變常規的施工測量方法,經緯儀必須進管。但管道在施工過程中是不斷向前移動的,因此測站的座標也是在不斷變化的。要在測站座標不斷改變的情況下,隨時隨地指出管道前進方向,這就是曲線頂管中管道定向測量要解決的中心問題。
解決的辦法有2個:
1.管道內布置多臺全站儀,依靠全站儀的優勢,在短時間內通過計算機確定每站經緯儀的方向,指出管道頂進方向。這一方法實質上是經緯儀導線法,方法可行但成本高。
2.管道內設置一臺普通經緯儀,一個覘標,2者均布置在工具管的后部。工具管上的標尺、經緯儀、后視覘標3者間保持一定的距離,并與管道固定,隨管頂進而跟進。經緯儀、后視覘標的中心坐標是根據事先測定的實際管軸線計算所得,工具管上的測點座標查設計軸線可得。依靠這3者的關系就可算出管道的頂進方向,并由經緯儀指向。管軸線的測定需要一臺全站儀,管道每頂進數10m,測定一次工具管后的管軸線,并輸入計算機。施工中可以根據頂進距離,推算出3者的即時坐標,通過計算機的運算,就能指出工具管頂進方向。采用這一方法,速度快、成本低,使用人力少。
上面分析了曲線頂管中的6個主要問題,還很膚淺,尚需各方面共同進一步研究完善。
本文關鍵詞: 頂管施工
上一篇:大口徑頂管施工出洞技術介紹
下一篇:頂管施工這種非開挖技術優點大于缺點